- La visite du Château ;
- Environnement paysager ;
- Album d'une visite ;
- La longue marche des tournesols : les photos de Jean Luc Andrzejewski ;
- Annabel ROMERO 2006 ;
- Visite de la famille du Costa-Rica ;
- Vu du Peyregal ;
- Les CataDivas 2019 ;
- La fête 2019 ;
- Couleur Soleil, 2018 ;
- Les cuivres Aerïs 2017 ;
- Christophe Roncalli 2016 ;
- Telle Mère, telle Fille 2015 ;
- Le Trio Bergin' et la chanson Française, 2014 ;
- CONTES DOPÉRA 2013 ;
- Pour que plus jamais ça ! 2012 ;
- Marcel et Raymonde, 2011 ;
- L'Opérette est dans le pré, 2010 ;
- Show de Divas, 2009 ;
- Les Fraises Salées, 2008 ;
- Casta Diva, Vox Populi, 2007 ;
- Sauvé des ruines ! ;
- La Société d'Histoire du Garnaguès ;
- Gaston Tissinier, chroniqueur, historien de la Piège ;
- Albert Salvetat s'en est allé... ;
- L'Association Namuka ;
- Le catharisme ;
- Le Pastel ;
- Déposition de Jehan d'Aulon ;
- Déportation d'Irma Jacoby ;
- Les de Mézerville au Costa-Rica ;
- Gaston Phébus, Comte de Foix ;
- Mézerville: étape gastronomique de la Piège ;
- Bibliographie ;
Le silence a régné dans la cour du château en 2020 en raison des contraintes sanitaires.
Espérons que la fête de Mézerville aura lieu en 2021 et que l’Association NAMUKA pourra
nous proposer un spectacle !
Nombre d'Or et Géométrie
Construction géométrique du nombre d'or
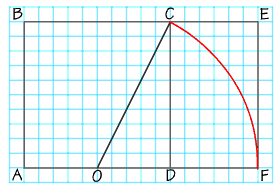
• Soit un carré ABCD
• O milieu de AD
• Un arc de cercle de centre O et de rayon OC coupe le prolongement de AD en F
• Le segment AF représente le nombre d'or
Calcul de AF
Dans le triangle rectangle OCD :
Si on définit : AD = AB = BC = 1
donc :
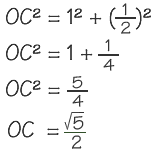
donc :
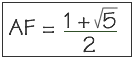
Le rectangle ABEF est dit "rectangle d'or" puisque ses côtés sont dans le rapport du nombre d'or
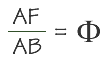
Nombre d'or et pentagone
Le pentagone régulier est un polygone régulier à 5 côtés inscrit dans un cercle et dont tous les côtés et tous les angles ont les mêmes mesures.
L'angle entre deux côtés consécutifs vaut 108°
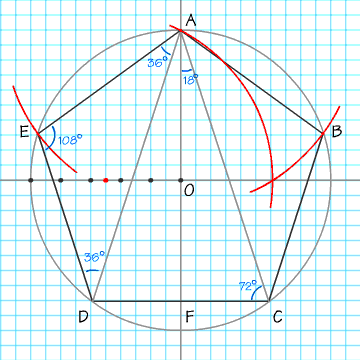
Soit le triangle ADC et les triangles ADF et AFC
Calcul de FD
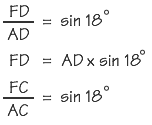
Soit DC = AD sin 18° + AC sin 18°
Soit DC = AD x 2sin 18°
DC = AD x 0,618
Le rapport entre une diagonale et un côté du pentagone est égal au nombre d'or
Les triangles AED et ADC sont des "triangles d'or" puisque leurs côtés sont dans le rapport du nombre d'or
Autre relation remarquable :
Spirale d'Or
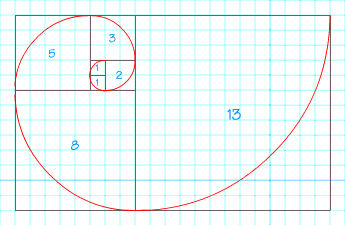
Les côtés des carrés sont une suite de Fibonacci
1, 1, 2, 3, 5, 8, 13 ...
La figure peut être construite à partir des rectangles d'or