Accueil ;

Visite du château ;

• La visite du Château ;

• Environnement paysager ;

• Album d'une visite ;

• La longue marche des tournesols : les photos de Jean Luc Andrzejewski ;

• Annabel ROMERO 2006 ;

• Visite de la famille du Costa-Rica ;

• Vu du Peyregal ;

Événements ;

• Les CataDivas 2019 ;

• La fête 2019 ;

• Couleur Soleil, 2018 ;

• Les cuivres Aerïs 2017  ;

• Christophe Roncalli 2016 ;

• Telle Mère, telle Fille 2015 ;

• Le Trio Bergin' et la chanson Française, 2014 ;

• CONTES D’OPÉRA 2013 ;

• Pour que plus jamais ça ! 2012 ;

• Marcel et Raymonde, 2011 ;

• L'Opérette est dans le pré, 2010  ;

• Show de Divas, 2009 ;

• Les Fraises Salées, 2008 ;

• Casta Diva, Vox Populi, 2007 ;

Eléments d'histoire ;

• Sauvé des ruines ! ;

• La Société d'Histoire du Garnaguès ;

• Gaston Tissinier, chroniqueur, historien de la Piège  ;

• Albert Salvetat s'en est allé... ;

Compléments ;

• L'Association Namuka ;

• Le catharisme ;

• Le Pastel ;

• Déposition de Jehan d'Aulon ;

• Déportation d'Irma Jacoby ;

• Les de Mézerville au Costa-Rica ;

• Gaston Phébus, Comte de Foix ;

• Mézerville: étape gastronomique de la Piège ;

• Bibliographie ;

Machines médiévales ;

• Introduction ;

• Grue sur pivot ;

• Enfonce-pieux ;

Curiosités géométriques historiques ;

• Présentation générale ;

• Tracé de l'heptagone ;

• Trisection d'un angle ;

• Tracé de l'enneagone ;

• Le Nombre d'Or ;

• Géométrie du Nombre d'Or ;

• La Quadrature du cercle ;

Contact ;

• Jacques Demichelis : les adieux ;

• Contact par formulaire ;

• Les propriétaires du château ;

• Localisation du Château ;

• Ouverture au public ;

• Liens ;

La Quadrature du cercle

Il s’agit de construire un carré dont la surface soit égale à celle d’un cercle.
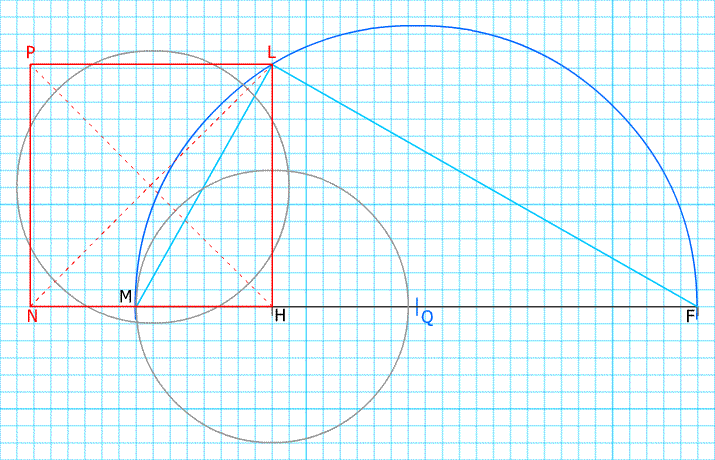
Si on choisit un cercle dont le rayon est l’unité, il faut tracer un carré dont le côté soit égal à puisque la surface du cercle est égale à .

Première Partie : Construction géométrique du nombre 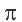d’après Kochansky

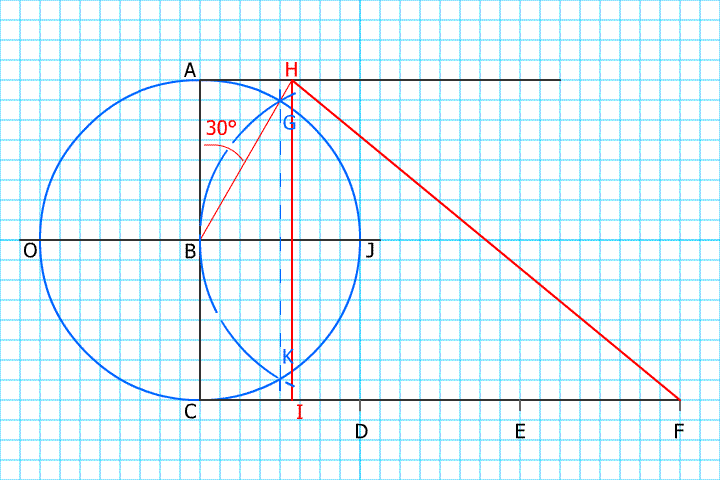
• Soit un cercle de centre B et de rayon BC = 1 (unité), deux diamètres perpendiculaires AC et OJ, deux perpendiculaires en A et C au diamètre AC.

• Sur la perpendiculaire à AC en C, on trace trois segments égaux
  
  CD = DE = EF = 1 (unité)
  

• Un arc de cercle de centre J, rayon JB = 1 (unité), coupe le cercle précédent en G et K, déterminant un côté du triangle équilatéral inscrit et par conséquence
  
  un angle (A B G) = 30°
  

• BG prolongé coupe la perpendiculaire en A en H.
  
  Le segment FH est égal à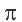
  

Démonstration :

• On trace la perpendiculaire IH à CF

• Dans le triangle ABH    tg 30° = AH/AB= 0,57735 (AB = 1 unité)

• Dans le triangle rectangle HIF,   HI = AC = 2 unités

• IF = CF – CI et CI = AH =  0.57735

• HI² +IF² = HF² (IF = 3 – 0.57735)

• HF² = 4 + (3 – 0.57735)²

• Soit : HF = 9,86923

• HF = 3,141533

Deuxième partie : construction géométrique de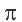

• Soit FH = 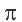, on prolonge FH en M tel que HM = 1 (unité)

• Soit Q milieu de MF

• Un arc de cercle MLF (centre Q)

• Une perpendiculaire  à HF élevée en H coupe l’arc de cercle en L,
  
  LH =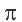
  

Démonstration :

Les triangles MFL et LHM sont rectangles et semblables : LH/HM = FH/LH

En conséquence :

• LH² = HM *FH, HM = 1 (unité)

• LH²= FH =

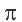
• LH  = 

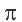
Conclusion :

La surface du carré LPNH dont le côté est égal àest proche de la surface égale àdu cercle de centre H et de rayon HM = 1.

Retour à l'index